Risk Yönetimi 03

Daha önceki yazılarda risk üzerine temel tanımlar ve belirsizlik altında karar alma ile beklenti teorisi çerçevesinde zaten biraz ilerlemiştik. Bugün ise beklenen getiri ve risk ölçümü için teorik çerçeve ile devam edelim. Konumuz uzun, vaktimiz kısıtlı olduğu için hemen notlara geçelim isterseniz. İçerik biraz daha yoğun ve sayısal ağırlıklı olduğundan belki ilerde örneklerle konuya tekrar döneriz.

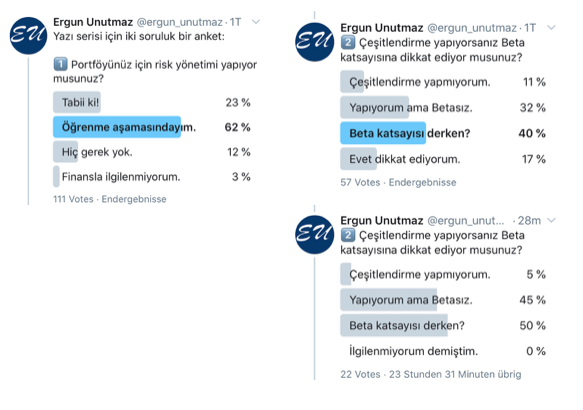
Öncelikle, Twitter üzerinden hazırladığım ankete katılan herkese teşekkür ederim. Bu tür sorularla içerik hem interaktif bir hâl alıyor, hem de daha spesifik bir alana yönelme şansı oluşuyor. Gelen sonuçlar bence oldukça iyi. Katılımcıların yüzde 85’i ya risk alanında önceden bir altyapı edinmiş ya da kendisini geliştirme aşamasında.

Risk konusu birçok alanda farklı şekillerde kullanılsa da finans dünyasındaki şekli oldukça karmaşık. Teknik kısımları hakkında bilgi sahibi olunsa bile uygulaması da ayrıca zahmetli olabiliyor. Tabii bir de konunun ne kadar gerekli olduğu tartışması var ki ona da ileride değineceğim. Ancak anketin devamından görünen o ki Beta Katsayısı ve uygulamasına bir kaç örnek vermek faydalı olacaktır.

Teorik Çerçeve

Markowitz, Portföy Seçim Modeli ile devrim gerçekleştirdiğinde,

“bir menkul kıymetin yatırımcı için değerinin, en iyi şekilde bu menkul kıymetin ortalaması, standart sapması ve portföyde bulunan diğer menkul kıymetlerle olan korelasyonu ile değerlendirilebileceğini”

önermişti. Yatırımcının gayesi, kabul edilebilir bir risk düzeyinde portföyün getirisini maksimize etmek ya da belirli bir getiriyi veri kabul ederek risk seviyesini azaltmak olmalıdır. Yatırımcının riske karşı tutumu yanında tek dönemlik yatırım varsayımı, portföyün getirisinin varyansı ya da standart sapması ile  riskin ölçümünü hesaplamayı mümkün kılmaktadır.

O hâlde ortalama, varyans ve standart sapma nedir, kısaca bir bakalım: 

Ortalama ile basit bir aritmetik işlemin sonucu kastedilmektedir ve bu sonuç istatistik alanında Yunan alfabesindeki µ (müğ) harfi ile gösterilir. Bir veri setindeki 1’den N kadar olan “x” değerlerinin  ortalaması bu “x” değerlerinin toplamının N sayısına bölünmesi ile hesaplanır.

Bir veri setindeki herhangi bir değerin, o veri setinin ortalamasından farkına ise “sapma” denilmektedir. 

Normal dağılımın bir sonucu olarak bazı veriler ortalamanın altındayken bazıları da üzerinde kalacağı için veri setindeki sapmanın ölçümünde ortalama almak (sonuç sıfır olacağı için) işe yaramayacaktır. Bu nedenle, sapmaların her birisi için kare alma işlemi yapılarak eksi değer sorunu giderilir ve ardından ortalama alınır. Varyans, işte bu işlem sonucunda elde edilen, Yunanca sigma harfinin karesi ile gösterilen, bir değişkenlik ölçütüdür.

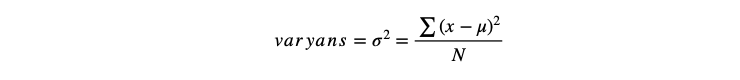
Burada dikkat edilmesi gereken nokta, matematiksel işlem sonrası hataların olduğundan daha büyük hâle gelmesidir. Dolayısı ile elde edilen sonucun kare kökünü alarak bu sorun da giderilmiş olur. Standart sapma, bu dönüşüm sonrası çıkan değer olup aslında risk olarak da ifade edebileceğimiz bir ölçü, istatistiki yorumlarda önemli bir rol oynayan işlemdir.

Bu bilgiler ışığında Markowitz’in yukarıda bahsettiği konuyu bir şekil yardımı ile açıklamaya çalışalım. Bir hisse senedine ait beklenen getiri ve hisse senedinin riski arasında doğrusal bir ilişki vardır. Standart sapma ile ölçülen risk unsuru arttıkça beklenen getiri de artacaktır.

Birden fazla hisse senedi ile oluşturulan bir portföyde kovaryansa da bağlı olarak hem beklenen getiri hem de standart sapma değişecektir. Beklenen getiriyi dikey eksende, standart sapmayı yatay eksende gösterdiğimizde; pozitif azalan eğimli mavi çizgi risk seviyesi arttıkça beklenen getirinin de arttığını, ancak belirli bir noktadan sonraki risklerin getiriyi daha fazla arttırmadığını ifade etmektedir. Dolayısı ile riskten kaçınan bir yatırımcı A noktasını tercih ederken risk arayan bir yatırımcı ise B noktasına kadar ilerlemeyi uygun görebilir. Portföy yönetiminde etkin sınır olarak tanımlanan bu durumu bir kenara not ederek şimdilik konuyu burada sınırlayalım.

Risk Türleri

Olabildiğince kısa tutmaya çalıştığım bu teorik çerçeveyi, piyasalarda işlem yaparken nasıl kullanacağız sorusuna yüzeysel olarak şöyle bir yorum yapabiliriz:

Bir varlığın portföyde taşınması ile en az piyasa ortalamasına eşit bir getiri elde etmek hedeftir, ki bunu yapabilmek bence başarıdır. Varlığın ya da portföyün getirisini arttırmak için riski arttırmak, ancak zararları önlemek için de optimal bir noktada durmak gerekmektedir.

Geçmeye çalıştığımız getiri oranı, risksiz faiz oranı olarak nitelendirilen uzun vadeli devlet tahvillerinin getirisi olduğuna göre bu ortalamadan ters yönde uzaklaşmak bir risktir ve zarar olarak hesaplarımıza yansıyacaktır. Bu ortalamadan pozitif ayrışmak ise yine risk olarak tanımlanmakta, ancak etkin bir donanım ile destekleniyorsa ilave bir getiri ile ödüllendirilmektedir.

O hâlde önce risk türlerini ayırıp neleri yönetebileceğimize bir bakalım:

Sistematik ve sistematik olmayan riskler olarak yapılan gruplandırmada; eğer bir olay, piyasadaki tüm aktörleri, ekonominin genelini ve tüm yatırım araçlarını etkiliyorsa söz konusu olan sistematik bir risktir. Sistematik olmayan riskler ise çeşitlendirme ile normalde yatırımcı tarafından önlenebilecek olan, varlığın kendisinden kaynaklanan risklerdir.

Deprem, doğal afet vb. olayları bir kenera koyarsak, sistematik risklerin alt kollarını jeopolitik, siyasi, ekonomik ve piyasa riskleri şeklinde başlıklarla izleyebiliriz. Bu tür riskleri için yapabileceklerimiz sınırlıdır. Farklı ülkelerde de yatırımlar yaparak riski dağıtmak bir çözüm gibi görünse de Covid-19 göstermiştir ki, küreselleşme sonucu artık farklı ülkeler ve piyasalar arasındaki bağ çok sıkıdır.

Asıl odaklanmamız gereken yer, farklı yatırım araçlarını içeren, farklı sektörlerde, güçlü altyapısı olan ya da büyüme potansiyeli yüksek şirketlerden oluşan dengeli bir portföy kurmaktır.  Portföy çeşitlendirmesi hakkında daha önce bir açıklama sunmuştum. Bir sonraki yazıda sistematik olmayan riski de içerecek şekilde bir örnek ve Beta Katsayısına ilişkin hesaplamalarla devam edeceğim. 

Kazançlı yatırımlar dilerim.

Ergun UNUTMAZ, 18.05.2020